Unit 3 parent functions and transformations homework 5 – Welcome to Unit 3: Parent Functions and Transformations, Homework 5! This engaging assignment delves into the fundamental concepts of parent functions and their remarkable transformations, empowering you to manipulate and analyze functions with precision.
Parent functions serve as the foundation for understanding a vast array of mathematical functions. They possess distinct characteristics and properties that define their behavior. Through transformations, we can modify these parent functions, creating new functions with altered graphs and applications.
Parent Functions

Parent functions are basic functions that serve as building blocks for more complex functions. They exhibit specific characteristics and properties that define their fundamental behavior. Common parent functions include:
- Linear functions: f(x) = mx + b
- Quadratic functions: f(x) = ax^2 + bx + c
- Exponential functions: f(x) = a^x
- Logarithmic functions: f(x) = log ax
Transformations of Parent Functions
Transformations are operations that modify the graph of a parent function without changing its basic shape. These transformations include:
- Translations: Shifting the graph horizontally or vertically
- Reflections: Flipping the graph across the x-axis or y-axis
- Dilations: Stretching or shrinking the graph horizontally or vertically
Transformations affect the graph of a parent function by:
- Moving key points (intercepts, vertices, asymptotes)
- Changing the direction of the graph
- Altering the steepness or width of the graph
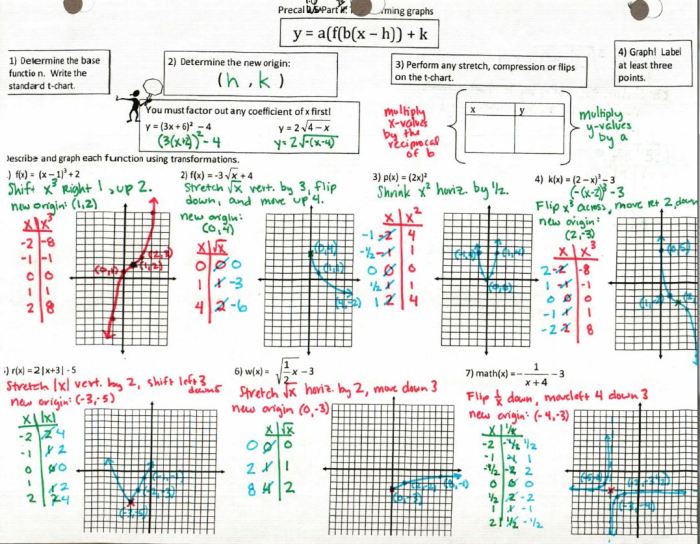
Applying Transformations, Unit 3 parent functions and transformations homework 5
To apply transformations to a parent function:
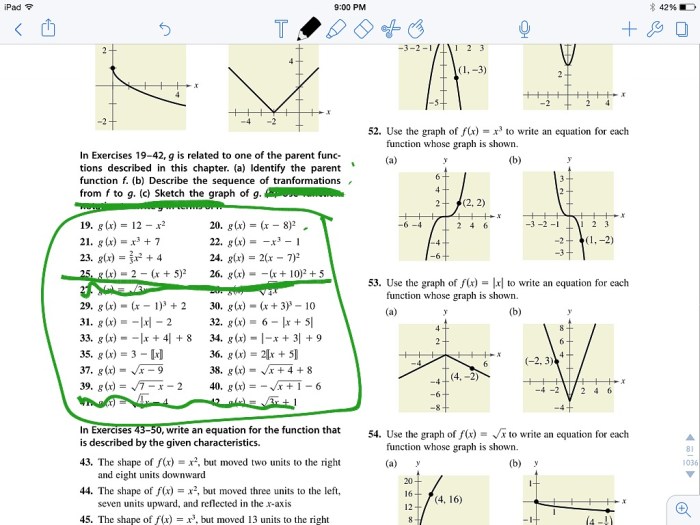
- Identify the parent function.
- Determine the type of transformation.
- Apply the transformation rules to the parent function equation.
For example, to translate the parent function f(x) = x^2 two units to the right, the transformation rule is f(x – 2) = (x – 2)^2.
Graphing Transformed Functions
To graph a transformed function:
- Graph the parent function.
- Apply the transformation rules to the graph of the parent function.
- Identify the key features of the transformed function (intercepts, vertices, asymptotes).
For example, the graph of f(x) = (x – 2)^2 is a parabola shifted two units to the right compared to the graph of f(x) = x^2.
Common Queries: Unit 3 Parent Functions And Transformations Homework 5
What is a parent function?
A parent function is a basic function that serves as a template for creating new functions through transformations.
What are the common types of parent functions?
Common parent functions include linear functions (f(x) = mx + b), quadratic functions (f(x) = ax^2 + bx + c), exponential functions (f(x) = a^x), and logarithmic functions (f(x) = log(a)x).
How do transformations affect the graph of a parent function?
Transformations can shift the graph of a parent function horizontally or vertically, flip it over an axis, or stretch or shrink it.