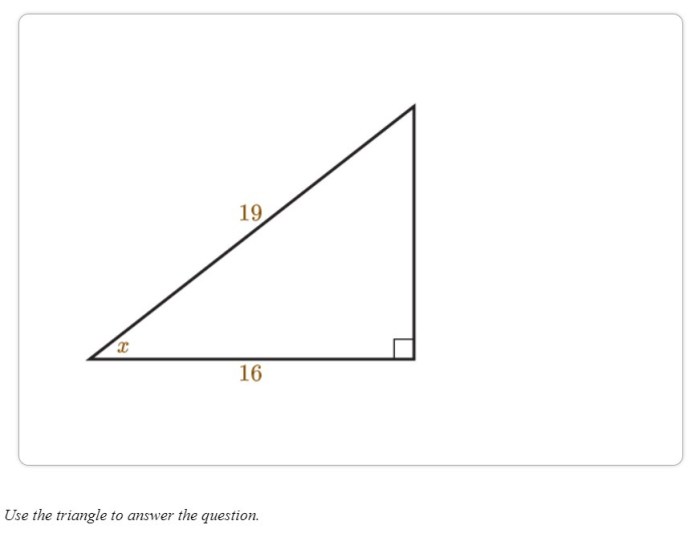
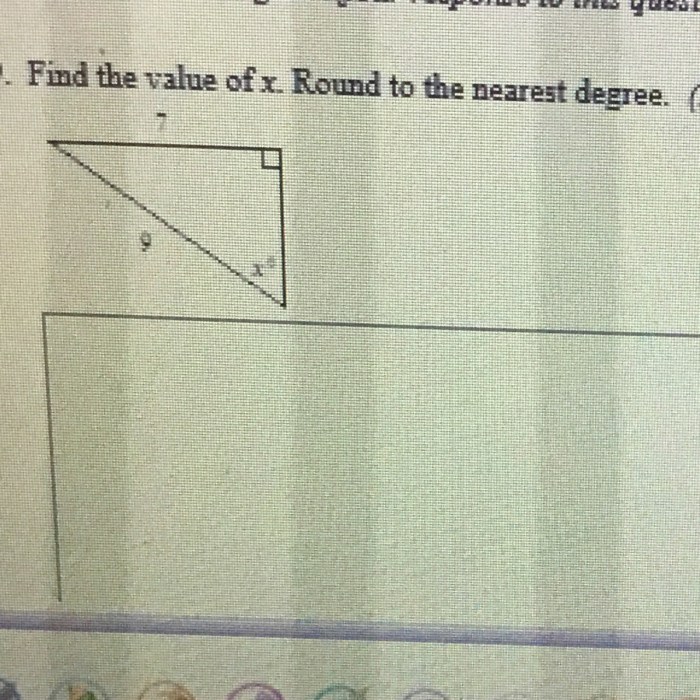
Find the value of x. round to the nearest degree is an essential mathematical concept that permeates various fields of study and everyday life. This guide delves into the intricacies of finding the value of x, exploring methods for solving equations, applications in geometry and calculus, and the significance of rounding to the nearest degree.
Understanding the concept of finding the value of x forms the foundation of this exploration, as we delve into the practical applications of this concept in solving algebraic equations and geometric problems. Furthermore, the role of trigonometric functions and derivatives in finding the value of x will be examined.
Finding the Value of x

Finding the value of x involves solving an equation or expression to determine the unknown variable x. It is a fundamental skill in mathematics, with applications in various fields such as algebra, geometry, trigonometry, and calculus.
In algebraic equations, x represents the unknown value that satisfies the equation. For instance, in the equation 2x + 5 = 15, the value of x can be found by isolating it on one side of the equation. By subtracting 5 from both sides, we get 2x = 10, and then dividing both sides by 2, we obtain x = 5.
Rounding to the nearest degree is a common practice in mathematics, especially when dealing with angles and trigonometric functions. It involves finding the closest integer value to the actual value of the angle, which is expressed in degrees.
Methods for Solving Equations
There are several methods for solving equations, including:
- Substitution method:Substituting the value of one variable in terms of another to simplify the equation and solve for the remaining variable.
- Elimination method:Adding or subtracting equations to eliminate one variable and solve for the other.
- Factoring:Decomposing an equation into smaller factors and solving each factor for the value of x.
Trigonometric Functions, Find the value of x. round to the nearest degree
Trigonometric functions (sine, cosine, tangent) are used to find the value of x in equations involving angles and triangles. The definitions of these functions are:
sin θ = opposite / hypotenusecos θ = adjacent / hypotenuse tan θ = opposite / adjacent
Using trigonometric functions, we can find the value of x in equations such as sin 30° = x/10, where x represents the length of the opposite side of a right triangle.
Applications in Geometry
Finding the value of x is crucial in geometry, particularly in solving problems involving triangles. The following table summarizes the formulas for finding the measures of angles in triangles:
| Angle | Formula |
|---|---|
| Interior angle | 180°
|
| Exterior angle | 180° + (sum of opposite interior angles) |
| Angle in a semicircle | 90° |
- Geometric problems involving finding the value of x:Finding the missing angle in a triangle, finding the length of a side in a triangle, finding the area of a triangle.
- Using trigonometry to solve geometry problems:Using trigonometric functions to find the length of sides or angles in triangles.
Applications in Calculus
In calculus, finding the value of x involves finding the derivative of a function and setting it equal to zero. The derivative of a function represents the rate of change of the function with respect to its input variable. By finding the value of x where the derivative is zero, we can find the critical points of the function, which can provide information about the function’s maximum or minimum values.
Example:Finding the critical points of the function f(x) = x^3 – 3x^2 + 2x by finding the value of x where the derivative f'(x) = 3x^2 – 6x + 2 is equal to zero.
Top FAQs: Find The Value Of X. Round To The Nearest Degree
What is the significance of rounding to the nearest degree?
Rounding to the nearest degree ensures accuracy and practicality in measurement and calculations, particularly in fields such as engineering, construction, and navigation.
How are trigonometric functions used to find the value of x?
Trigonometric functions, such as sine, cosine, and tangent, establish relationships between angles and sides of triangles. By utilizing these relationships, we can solve equations involving angles and find the value of x.
What is the role of derivatives in finding the value of x?
Derivatives, a concept in calculus, measure the rate of change of a function. They can be used to find the maximum or minimum points of a function, which can aid in finding the value of x.